👉🏻 Clicca qui per guardare la versione video su YouTube 👈🏻
Dietro ogni transazione Bitcoin c’è una matematica elegante e impenetrabile. Ma soprattutto incomprensibile… fino ad oggi! In questo episodio entriamo nel cuore della crittografia: dalle curve ellittiche all’ECDSA, la firma digitale che protegge i tuoi BTC.
Episodio 7 di 10 della serie sulla crittografia Bitcoin. Recupera qui gli altri episodi della serie 👉🏻 Caccia al tesoro
🔑 Perché la matematica è il cuore di Bitcoin?
Immagina che quando qualcuno ti chiede un bonifico non deve preoccuparsi che tu abbia veramente i soldi sul conto, ci pensa la banca a permettere l’invio se ci sono i fondi o a negarlo se i fondi non ci sono. Tutto il processo è sicuro e garantito dalla banca.
Quando invii una transazione Bitcoin, NESSUNO può conoscere qual’è la tua chiave privata (altrimenti potrebbero spendere i tuoi BTC), hanno a disposizione solamente la tua chiave pubblica.
Ma se le chiavi pubbliche sono per l’appunto, pubbliche, come faccio a dimostrare che il saldo che tu vedi su quella chiave pubblica è realmente mio?! Come faccio a dimostrarti di essere il possessore di quella chiave pubblica, senza però svelarti la chiave privata associata?!
Ma se le chiavi pubbliche sono per l’appunto, pubbliche, come faccio a dimostrare che il saldo che tu vedi su quella chiave pubblica è realmente mio?! Come faccio a dimostrarti di essere il possessore di quella chiave pubblica, senza però svelarti la chiave privata associata?!
Ma soprattutto, se io conosco i calcoli che mi portano ad avere quella chiave pubblica, come mai non è possibile fare l’operazione inversa e dalla chiave pubblica risalire a quella privata che gestisce tutti i fondi?
La sicurezza per non svelare mai la chiave privata si basa su un principio fondamentale:
Calcolare la chiave pubblica è facile.
P = k ^ G
Dove: P = chiave pubblica, k = chiave privata, G = costante, numero ben preciso, pubblico, che dopo vedremo.
Eppure, scoprire k sapendo P e G è praticamente impossibile.
Lo so che sembra strano, sembra una normale potenza, ma non è così. Andiamo a scoprire la base della crittografia a curva ellittica (ECC) utilizzata in Bitcoin.

🔒 Dalla crittografia classica all’ECC
Andiamo per gradi, prendiamo il caso di Alice e Bob che vogliono scambiare dei Bitcoin.
- Alice, la cui firma chiameremo “A”, ha un suo segreto “a”, es: “2”
- Bob, la cui firma chiameremo “B”, ha un suo segreto “b”, es “3”
- Entrambi scelgono di utilizzare un un numero pubblico “G”, es: “5”, per creare la firma
A = G ^ a (G elevato ad “a”)
B = G ^ b (G elevato a “b”)Quando Alice e Bob si scambiano la firma A e B, è veramente facile per entrambi ricavare il segreto a o b essendo a conoscenza sia della firma che del numero pubblico.
A = 5^2 = 25
Ma se io avessi:
25 = 5^a per calcolare “a” devo:
- andare a tentativi, (ed immagina farlo con un numero di 77 cifre come in bitcoin)
- oppure fare un logaritmo, serve per forza un calcolatore
Ora, partiamo con il risolvere il problema n.2, cioè dobbiamo fare in modo che anche per un computer sia impossibile fare l’operazione inversa tramite il logaritmo.
Per fare questo dobbiamo introdurre un elemento, così ecco che viene un ulteriore componente: il modulo, “mod p”, capiamo il perchè:
A = (G ^ a) mod p
B = (G ^ b) mod p“Mod” sta per modulo, serve per fare aritmetica su un campo finito.
In pratica: prendi il resto della divisione tra (G^a) e p
Immagina un orologio, ha 12 ore quindi è mod 12, cioè i numeri vanno a ruota da 1 a 12 e si ripetono sempre così.
Se sono le ore 10 e passano 5 ore allora saranno = le ore 3
Stessa cosa sempre prendiamo i nostri valori: A = G^a mod 12 ovvero A = 25 mod 12 ovvero A = 1
Perchè 25 / 12 = 2 con il resto di 1
Se quindi io ho: (G^a) mod p = A ed io conosco G, p, A
L’unico modo per calcolare “a” è andare per tentativi. Questo si chiama il “discrete log problem”.
Ora, un computer abbastanza potente, non avrebbe problemi a fare milioni di tentativi al secondo, quindi ci sono solo 2 soluzioni:
- Usare dei numeri infinitamente grandi
- Non usare dei numeri…
La soluzione numero 1 ha un problema, i numeri non possono essere così grandi, noi abbiamo bisogno di poter usare questi numeri anche in dispositivi che hanno potenze di calcolo inferiori ad un supercomputer.
Di conseguenza si procede con l’opzione numero 2, non usare dei numeri ma dei punti sui assi cartesiani, ecco perchè:
Riprendiamo l’esempio di prima “ A = G ^ a “ e sostituiamolo con i valori immaginati prima, otteniamo:
A = 5^2 = 5 * 5
B= 5^3 = 5 * 5 * 5
Sarebbe molto facile fare un’operazione con questi valori.
- Se io devo sommare 1 + 1 = 2, tutto molto facile
Ma se io devo sommare due punti su un grafico, X = ( 1 , 1 ) e Y = ( 2 , 2 )
- La somma dei 2 punti è qualcosa di più complesso di un’operazione matematica
🌈 Le curve ellittiche spiegate facile
Una curva ellittica è una funzione matematica del tipo:
y² = x³ + ax + bCioè che viene fuori per i vari valori dei punti x e y è una curva di questo tipo (ecco perchè il nome curva ellittica).
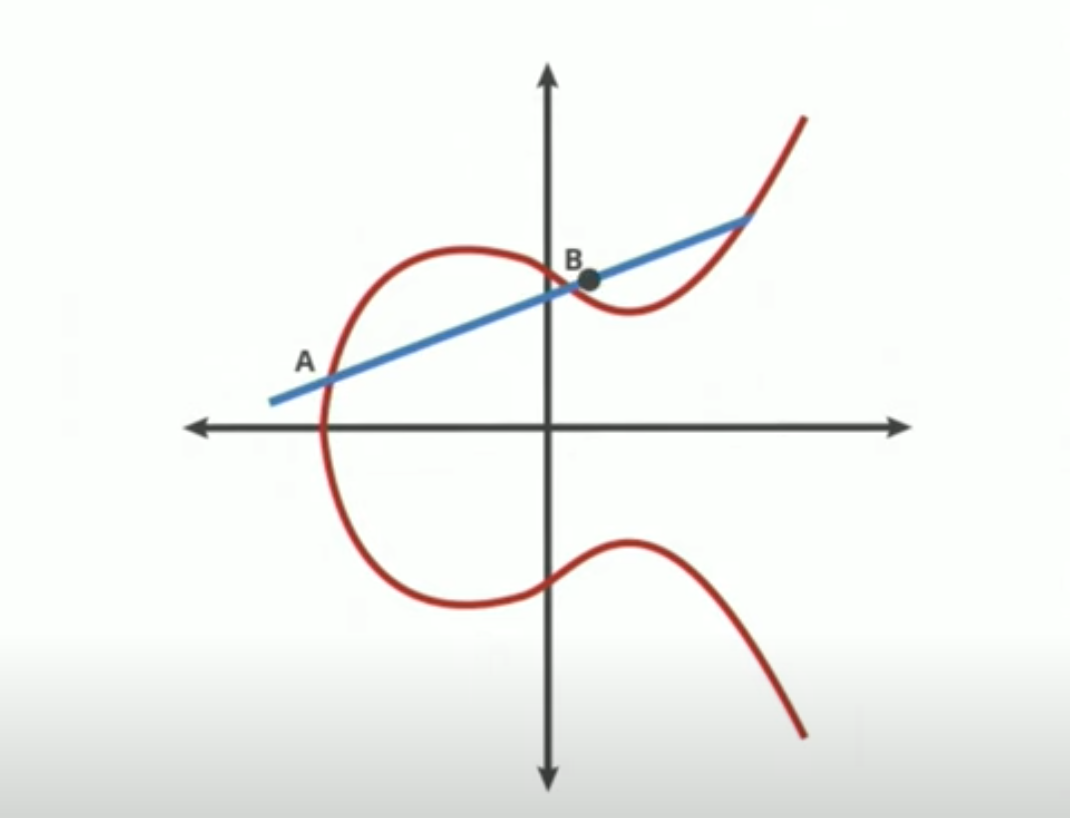
È usata in crittografia perché ha una proprietà speciale:
- Se prendi due punti sulla curva, A e B, la retta che li unisce incontrerà la curva in un terzo punto.
- Riflettendo questo punto rispetto all’asse x ottieni un altro punto C.
- Definendo A + B = C, questa operazione diventa una “somma” speciale.
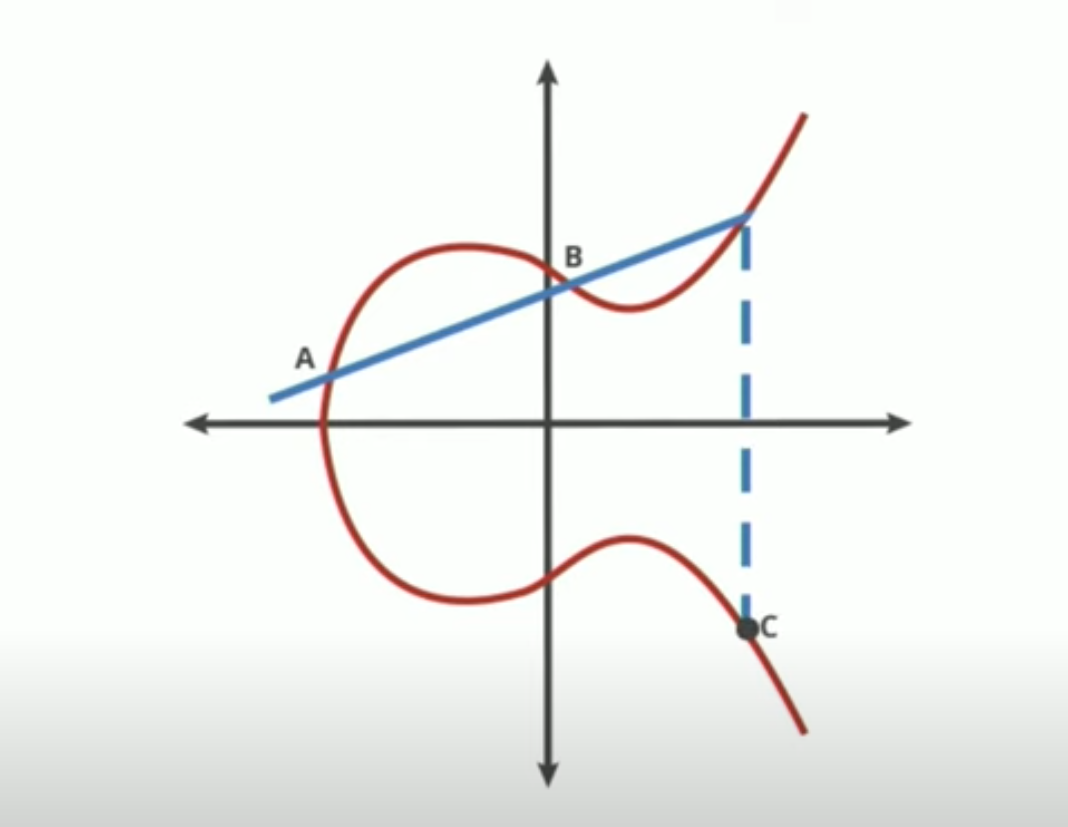
Se prendi un punto ben definito, chiamato punto G (punto di generazione) e lo “sommi con se stesso” k volte, ottieni un punto ben preciso, quel punto preciso è la tua chiave privata.
Questa operazione è abbastanza facile da fare, dunque se tu conosci k (cioè hai la tua chiave privata), allora ricavarne la chiave pubblica è un gioco da ragazzi.
Ti basta sapere quante volte devi trovare nuovi punti sulla curva.
Per completezza di informazioni G è un punto con queste coordinate:
- x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
- y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
Spero che questo esempio ti renda l’idea di che numeri ci sono in gioco e perché i calcoli sono molto complessi.
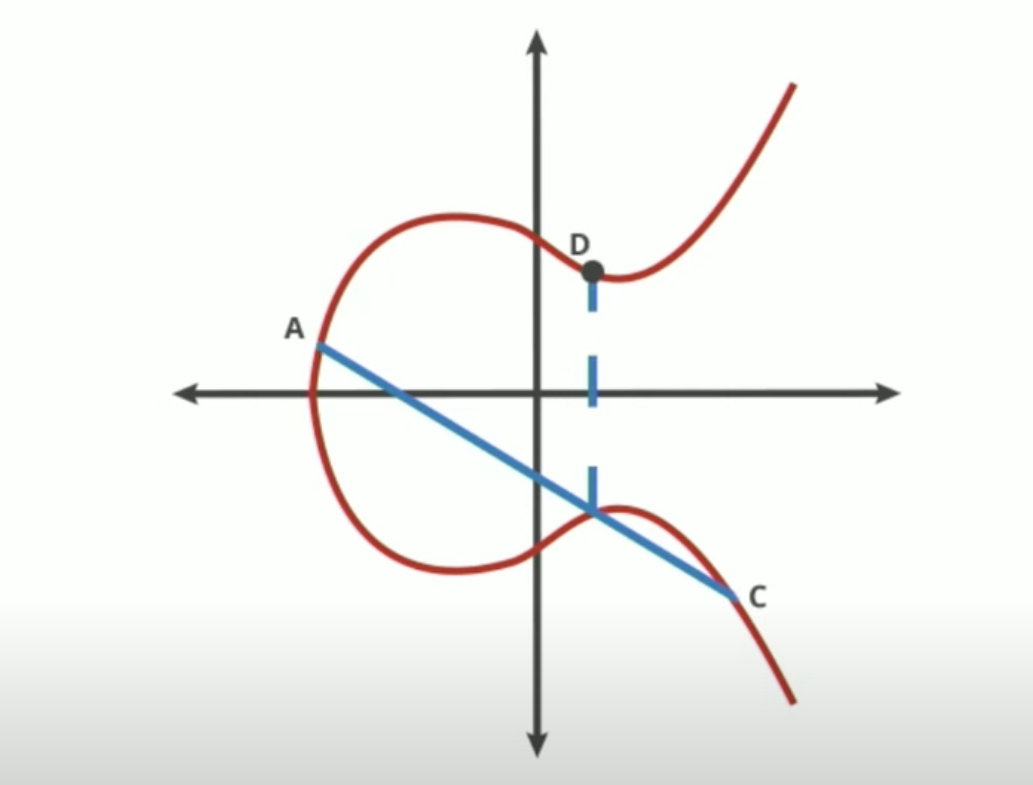
Ti ricordo che P e G sono dei punti, non numeri semplici, e così trovare k(chiave privata), cioè quante volte devi sommare G per ottenere P(chiave pubblica), è un problema matematicamente mostruoso: il logaritmo discreto ellittico.
È così difficile che nemmeno i supercomputer moderni possono farlo, se k è abbastanza grande (≈ 2²⁵⁶ possibili valori).
La crittografia a curve ellittiche è così potente perchè:
- Sicurezza enorme con chiavi piccole: un sistema ECC a 256 bit è sicuro quanto un RSA da 3072 bit.
- Efficienza: ideale per smartphone, hardware wallet e sistemi a basse risorse.
- Matematica elegante: la struttura delle curve rende impossibile invertire P = k × G.
L’ultima cosa che mi rimane da spiegarti è: come fa un estraneo che conosce la mia chiave pubblica a sapere che io possiedo la chiave privata associata?!
Il discorso è ovviamente complicato ma in sostanza quando firmo qualcosa con la mia chiave privata, io sto facendo dei calcoli che mi portano ad avere un punto di coordinate ben precise (questo punto dipende ovviamente dalla chiave privata e dal messaggio).
Chi verifica, riceverà un punto di coordinate (x,y) ed utilizzerà quelle coordinate per fare dei calcoli con la chiave pubblica e vedere se i suoi X e Y coincidono con quelli del firmatario.
In questa maniera si può verificare senza essere a conoscenza del dato originale.
📌 Prossimo episodio
Nel prossimo episodio parleremo di indirizzi Bitcoin e del perché alcuni iniziano con 1, altri con 3 o bc1, capendo le differenze tra P2PKH, P2SH, SegWit e Taproot.
Episodio 7 di 10 della serie sulla crittografia Bitcoin. Recupera qui gli altri episodi della serie 👉🏻 Caccia al tesoro
🤬 La parola di oggi è: 7. usanza



